|
A.N.Morozov
WATER-SALT REGIME FORECAST METHODS.
Reasoning from the set goals and considering technical possibilities
for realization of the tasks being solved, the models have been used,
in those a comparatively simple mathematical tool is applied, which
represents the main mechanisms of moisture and salt transfer.
Balance models apply known ideas of moisture balance in a certain
soil layer. The following dependences are in its basis:

|
1)
|
here
Q -irrigation; O -precipitation; E - total evaporation; I -moisture
exchange of the root-inhabited zone with lower layers; G -water
discharge to lower horizons. It is supposed that the all variables
are deterministic, and there are functional dependences upon time
and moisture. In particular, total evaporation:
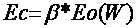
|
(2) |
here -  parameter
characterizing vegetation influence; Eo -evaporability; W -moisture
reserves in the soil. parameter
characterizing vegetation influence; Eo -evaporability; W -moisture
reserves in the soil.
The
dependence of replenishment from the lower horizons can be approximated:
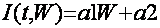
|
(3) |
here
-  , ,  - constants, are determined through modeling.
- constants, are determined through modeling.
Mineralization computation is carried out according the root-inhabited
zone?s salt balance equation:
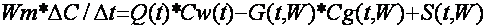
|
(4) |
here,
Cv - irrigation water mineralization; Cq - soil moisture mineralization
that comes to the lower horizons; S - convection-diffusion salt
transfer from the lower horizons, is approximated by the dependence:
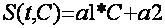
|
(5) |
For
moisture arrival time, one ought to check whether it will result
in saturation of the root-inhabited zone up to field moisture capacity
and further moisture discharge to the lower horizons.
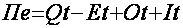
|
(6) |
The
value calculated is compared to the moisture deficit Ot in the root-inhabited
zone:

|
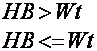 |
(7) |
if there
is irrigation water excess (Pt > Ot), discharge to the lower
horizons arises, and in the root-inhabited zone, moisture is formed,
which is equal to the field moisture capacity ? HB. If there is
no water excess (Pt < Ot), the irrigation water is accumulated
in the aeration zone:
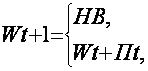
|
 |
(8) |
The
discharge is:

|
(9) |
otherwise,
Gt = 0
Crop capacity is determined by the formula:

|
(10) |
here,
-  number of "stressful"
days j for jth time interval; - number of "stressful"
days j for jth time interval; -  dimensionless reduction factor of crop capacity characterizing crop
decrease per one "stressful" day j of jth time interval
(
dimensionless reduction factor of crop capacity characterizing crop
decrease per one "stressful" day j of jth time interval
( ). ).
Stress days are determined as days in those the total soil moisture
potential Pt exceeds the critical level (see below).
In the first model modification, water-salt balance of the field
is computed and the design crop capacity is defined subject to the
given conditions and irrigation regime assigned.
The first modification, using the previous model, determines an
irritation regime excluding crop losses, but without taking into
account reducing income from costs for irrigation and water itself.
The third modification model carries out searching for the optimal
from economic standpoint irrigation regime. A standard inter-irrigation
regime is set therein, as it is in common practice mostly, and several
possible irrigation rates. The program makes full searching of all
probable combinations of irrigation rates and terms for a vegetation
period, and then selects the most efficient.
The imitation model of moisture and salt transfer in soil based
on the researches of L.M.Reks, I.P.Aydarov, A.I.Golovanov, and other
authors as well is described in detail in the work by V.A.Zlotnik
and A.N.Morozov (1983).
Two interconnected blocks are used in the model:
- one of water regime which forecasts moisture and filtration rate;
- one of salt regime that forecasts salt transfer.
The flow scheme of modeling of soil water-salt regime (WSR) state
and irrigation regime control is shown on figure 1.

Input
information in the form of soil-meliorative and climatic indices,
characteristics of irrigated lands state, technical features of
the hydromeliorative service, and crop requirements to growth conditions
is processed in state forecasting blocks, is controlled by the control
block which, in the case of need, issues commands to make vegetation
irrigation.
The known equation of moisture transfer accepted in the model looks
as follows:
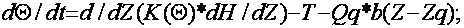
|
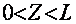 |
(11) |
here,
t - day time;
Z - vertical coordinate, m;
K( 0) - hydraulic conductivity factor, m/day;
T(Z,t) - moisture withdrawal rate by plant roots, m3/day per ha;
Qq - drainage effluent, m3/day per ha;
O - volume moisture;
H(Z,t) - water head, m;
b - delta function.
Target function is and H. Vertical filtration rate used in salts
transfer calculation is determined via the formulae:
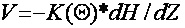
|
(12) |
Boundary
conditions on soil surface are specified by an irrigation regime
ensuring certain fixed conditions in the root-inhabited layer. The
decision describes changes of moisture and filtration rate used
further for the salt transfer calculation. The equation defining
C(Z,t) concentration in the salt transfer model is as follows:
|
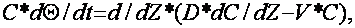
|
|
|
(13)
|
here,
D - hydraulic dispersion factor;
Zq - drainage location depth.
The value of hydrodynamic dispersion factor is computed through
the dependence:

|
(14) |
here,
Do - salts molecular diffusion factor;
^ - dispersion parameter
Salts
flow in the aeration zone is calculated by the formulae:
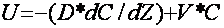
|
(15) |
Solving
the assigned task gives a forecast of pore solution mineralization
and the value of salt carry-over to drainage along with infiltration
feeding. When solving the task, a few functions are applied, which
determine:
- hydraulic conductivity factor;
- dependence of moisture capillary-sorption potential in soil;
- evaporation and transpiration dependence upon soil moisture;
- dependence of drainage effluent on the effective head value.
Dependence of the hydraulic conductivity factor on moisture K(O)
is taken by the S.F.Averyanov? formulae (1978). At that, K(O) is
determined via the filtration factor (Kf), porosity (m), moisture
of plant growth delay (PGDM):
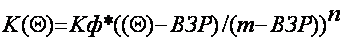
|
(16) |
The
exponent n, according to analyses of a number of researchers? actual
data, can be accepted in the range of 2-7 depending on soil constituent
stratum properties, and can be selected in such a way that to provide
the best approximation of the experimental data.
Dependence of the soil moisture capillary-sorption potential Y(O)
is accepted single-valued (without consideration of the hysteresis)
and must be determined for every soil constituent stratum. It is
set in a table form.
Head dependence on moisture is written as follows:
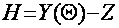
|
(17) |
To calculate
plants transpiration, in view of extreme approximateness of the
experimental data, a model with constant rate of moisture withdrawal
by the roots in depth (S.V.Nerpin and others, 1976):

|
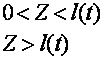 |
(18) |
here,
Ec(t) - evapotranspiration, mm/day;
a(t) - physical evaporation part.
Evapotranspiration value is computed taking into account soil moisture
by the GGI methods (Recommendations on evaporation calculation form
the land surface, 1976), applied for the conditions of the Central
Asia region (D.F.Solodennikov, 1981):
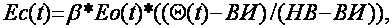
|
(19) |
here,
…®(t) - evaporability from water surface, mm/day;
 - factor representing
crop peculiarities in a certain vegetation period; - factor representing
crop peculiarities in a certain vegetation period;
ECM - evaporation cessation moisture;
LMC - least moisture capacity.
The drainage effluent value is approximated by a linear function
of the effective head (A.I.Golovanov, 1975):

|
(20) |
here,
A - drainage degree factor, l/day;
h(t) - groundwater depth, m.
Conditions and parameters of relation between groundwater and head
water horizons are defined by materials of hydro-geological investigations
with operation observations.
Assignment of regular fixed-rate irrigation, providing agro-technical
conditions in the root-inhabited layer, is made in the model by
the irrigation control block. Irrigation is automatically assigned
every time when the total potential in the soil moisture, expressed
via the equivalent pressure (Pc) and determined as the average value
in the root-inhabited layer l(t), reaches the critical value (Pk)
in the current time (see above).
Conditions for irrigation assignment is written in the form:
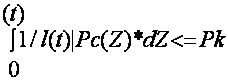
|
(21) |
here,
Pc(Z) = |P(Z)| + 0.36*C(Z),
P(Z) - capillary-sorption potential in soil moisture;
C(Z) - soil solution mineralization.
This task is solved by the numerical method, using the conservative
difference scheme (A.A.Samarskiy, 1977; G.I.Marchul, 1977), and
realized in FORTRAN-77 language.
Adaptation of these models through field determination of the parameters
specifically characterizing soil conditions in the area of the use
can considerably promote settling problems related to all possible
water saving per a crop unit produced.
How
to get in touch with us?
Return
to the main page
|

